
On the right-hand side, we need to have the plus or minus the square root of the value 24. That in this case is going to be the x minus 3.
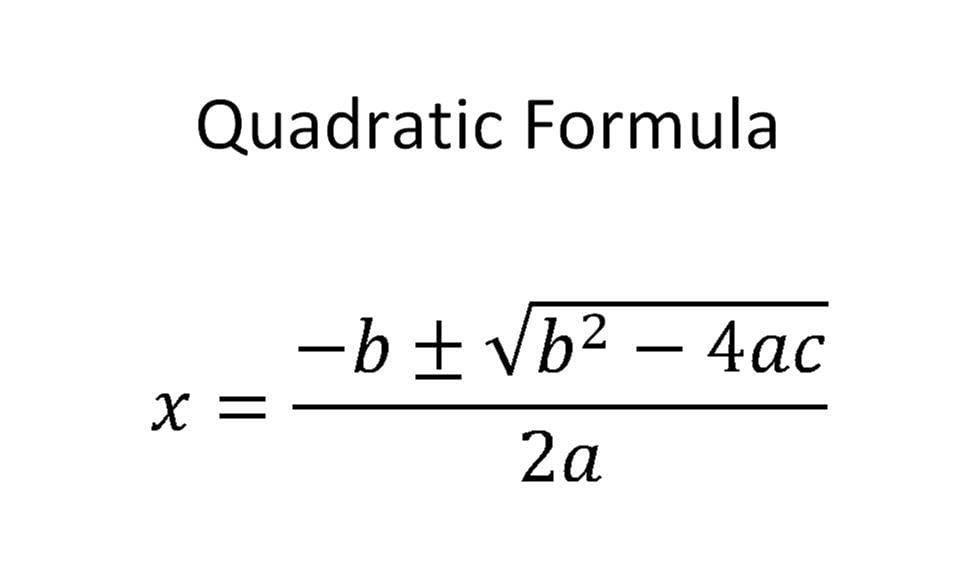
On the left-hand side, when I take the square root of something squared, I'm just left with what we could call the base. I'm now going to use the square root method, which is to take the square root of both sides of this equation. This means that this involves all of my variables, it's a perfect square, and it equals a constant. If I start off with the equation x minus 3 quantity squared equals the value of 24, then what I have is on one side of the equation a perfect square. I'm going to state it a little bit differently now. We're going to look at a second example where we're going to use, again, the square root method, which is just taking square root of both sides of the equation. And of course, we saw those two solutions in this format. So we're going to end up with x equals plus or minus the value of 4. And that's going to give us the value of 4. Now, the square root of 16 would be the number which when squared gives us 16. The symbolism with the radical sign if used without the plus minus just means the principal square root, which means the positive value. And what we can think of in the format of the equation when we solve it is to say that if we're solving for x, x is going to equal plus or minus, giving us both the positive and the negative, square root of 16. So there's a positive square root of 16 and a negative square root of 16. But it turns out that if I start off with negative 4 and square that, we also come up with 16. That is, if I take the value of 4 and square it, we end up with 16. It turns out that we end up having two square roots for a number. What numbers when squared would give us the value of 16? And I'm sure that what you're thinking right now is, I know that answer. Now, you probably can solve this by inspection.
So I have a perfect square, x squared, equals a constant value of 16. There are no other variable terms in this equation. A couple things to point out- we have the variable x squared isolated on one side of the equation. So now let's begin with the idea of a square root method on an equation that looks something like this, if we have x squared equals the value of 16. And then finally, we'll look at solving quadratic equations by using the quadratic formula. This is going to include a process called "completing the square." Then we'll move on and look at solving quadratic equations by factorization. The first one is going to be by the square root method. Now, in this session, we want to look at three different methods for solving these quadratic equations. So notice that this last part will tell us that we'll definitely have an x squared term in our equation. A quadratic equation in one variable, x, is an equation that can be written in the form ax squared plus bx plus c equals 0, where the values of a, b, and c are just constants and the value of a does not equal 0. Let's now review what a quadratic equation actually is. During this session, we're going to investigate the different methods we can use to solve quadratic equations in one variable.


 0 kommentar(er)
0 kommentar(er)
